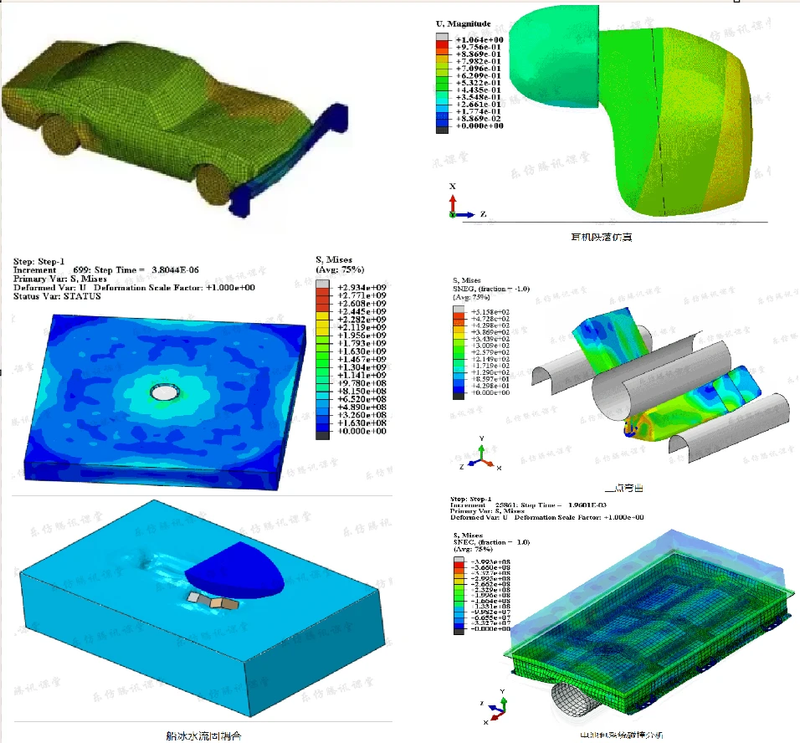
简介:本文档为初学者提供了一份关于ANSYS有限元分析的全面介绍,涵盖了有限元方法(FEM)的基础知识、软件操作流程及机械结构仿真分析。内容包括有限元方法在工程问题中的应用、ANSYS软件的使用、模型构建、材料属性设置、网格划分、边界条件与载荷定义以及结果分析和解释。旨在帮助学习者通过系统学习提升解决实际工程问题的能力。
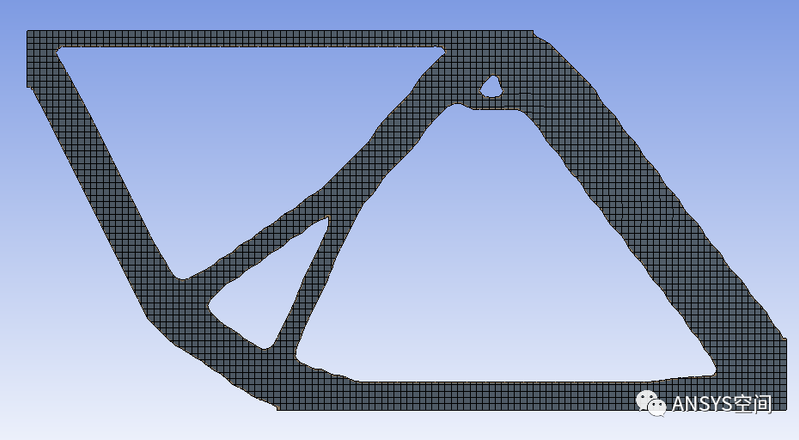
1. 有限元方法(FEM)基础 1.1 有限元方法概述
有限元方法(Finite Element Method, FEM)是一种强大的数值分析技术,广泛应用于工程领域中的复杂结构分析。它通过将连续的结构划分为许多小的、简单的元素,这些元素通过节点相互连接,在这些节点上应用已知的载荷和边界条件来求解整个结构的响应。
1.2 FEM的工作原理
在有限元分析中,首先需要根据实际问题来建立数学模型,然后将连续的结构离散化为有限数量的元素,这些元素通过有限数量的节点相连。接下来,选择合适的位移函数来近似描述每个元素内部的位移分布。利用变分原理或者最小势能原理,可以推导出每个元素的刚度矩阵和载荷向量,再根据整个结构的节点联系,综合起来形成整个结构的全局刚度矩阵和载荷向量。最后通过求解这组线性方程,可以得到结构的位移、应力、应变等信息。
1.3 FEM在工程应用中的重要性
在产品设计和工程分析中,准确预测材料和结构在载荷下的表现至关重要。有限元方法因其灵活性和准确性,在结构强度分析、热分析、流体动力学、电磁场分析等方面得到了广泛应用。FEM不仅可以帮助工程师优化设计,减少材料成本,还可以预防潜在的失效风险,从而提高产品的可靠性和安全性。
2. ANSYS软件操作流程 2.1 ANSYS软件界面介绍 2.1.1 软件界面布局与功能区域划分
ANSYS软件是一个功能强大的有限元分析工具,它为用户提供了一个集成化的工作环境,以支持从建模到分析和后处理的整个流程。软件界面布局设计得直观易用,方便用户高效地完成各项工作。界面主要可以分为以下几个区域:
在进行有限元分析工作之前,熟悉软件界面布局与功能区域的划分是至关重要的,这将帮助用户更高效地利用软件的各项功能。
2.1.2 基本操作与命令行输入
ANSYS提供了两种操作模式:图形用户界面(GUI)和APDL命令行。GUI操作直观简单,适合新手用户;而APDL提供了更大的灵活性和控制精度,适合高级用户进行更复杂的操作。在这一部分,我们将简要介绍如何在ANSYS中使用命令行输入。
使用命令行输入,用户可以通过编写一系列的APDL命令来控制软件行为。例如,创建一个简单的3D立方体模型可以通过以下命令实现:
/PREP7
*CREATE, rect, box, 0, 0, 0, 1, 1, 1
FINISH
每行命令解释如下: - /PREP7 是进入前处理模式的命令。 - *CREATE 是一个创建命令,这里用于生成一个名为 rect 的立方体,其顶点坐标为 (0,0,0) 和 (1,1,1)。 - FINISH 命令用于退出当前处理模式。
通过这种方式,用户可以编写更长的APDL脚本来完成复杂的操作,比如自动化模拟流程、参数化建模等。命令行输入虽然看起来复杂,但它为高级用户提供了一种强大的工具来精确控制分析过程。
2.2 ANSYS工作流程概述 2.2.1 前处理、求解与后处理基本步骤
在ANSYS中进行一个有限元分析,通常涉及以下几个基本步骤:
前处理 :定义几何模型、材料属性、网格划分以及边界条件和载荷设置。 求解 :提交分析计算,软件会根据设置的参数和条件运行求解器,求解物理问题。 后处理 :分析结果,提取有用信息,如位移、应力、温度分布等,并进行可视化展示。
这个工作流程是ANSYS软件的核心,无论是简单的静力学分析还是复杂的多物理场耦合仿真,都需要遵循这三步流程。对初学者来说,掌握这个流程是完成有限元分析的基础。
2.2.2 工程文件的管理与保存
在进行有限元分析时,工程文件的管理至关重要,它不仅涉及数据的保存,还包括历史记录的追踪、数据共享和版本控制。ANSYS提供了一系列工具来帮助用户管理这些文件:
在进行复杂的项目时,合理的文件管理策略能够帮助用户追踪项目进度,避免数据丢失,同时也方便团队成员之间的协作。
2.3 ANSYS软件操作实例 2.3.1 实体建模与参数化设计
ANSYS允许用户通过参数化建模来创建复杂的几何形状。参数化设计使用变量和参数来定义模型的几何特征,从而使得设计过程更加灵活和可调整。以下是一个简单的例子,通过参数化方式创建一个参数化的矩形板模型:
/PREP7
width = 100
height = 50
thick = 5
rect_prism, width, height, thick
FINISH
在这个例子中, width 、 height 和 thick 都是参数,分别代表矩形板的宽度、高度和厚度。使用 rect_prism 命令来创建一个长方体,其尺寸由这些参数决定。
通过改变参数值,可以快速生成一系列相似的设计方案,这对于设计优化和灵敏度分析非常有用。参数化模型不仅提高了建模效率,还增强了模型的可重用性。
2.3.2 分析类型的设置与计算流程
有限元分析中选择合适的分析类型至关重要,因为它决定了求解器将如何处理模型和计算结果。ANSYS支持多种分析类型,包括结构分析、热分析、流体动力学分析等。以下是一个结构静力学分析的基本设置步骤:
定义材料属性 :为模型指定材料,比如材料的弹性模量和泊松比。 网格划分 :根据模型的几何形状和所需的精度进行网格划分。 设置边界条件和载荷 :定义模型上的支持点、固定点、作用力等。 求解设置 :配置求解器的相关参数,如收敛准则和迭代次数。 求解计算 :运行求解器得到模型的应力、位移等结果。
下面是一个简单的APDL命令脚本,执行上述分析:
/SOLU
ANTYPE, 0 ! 静态分析
SOLVE ! 求解计算
FINISH
执行这段命令后,ANSYS求解器会开始计算,完成分析后,用户可以进入后处理阶段,对计算结果进行详细的查看和分析。
在本章节中,我们介绍了ANSYS软件的基本界面和工作流程,以及通过实例演示了如何进行实体建模和执行分析。通过这些步骤,用户可以开始对简单的模型进行有限元分析,并进一步深入学习更复杂的仿真流程。随着对软件使用的逐渐熟练,用户将能够完成更加精细和专业的仿真任务。
3. 机械结构仿真分析 3.1 机械结构分析的理论基础
在分析机械结构时,我们必须了解应力、应变以及本构关系的理论。应力是单位面积上的内力,它描述了物体内部各点受到的内力大小和方向,应变则描述了物体在外力作用下发生的形变。而本构关系则解释了材料在受到外力作用时应力与应变之间的数学关系。这些理论为我们预测和分析机械结构在不同工况下的表现提供了基础。
3.2 仿真分析的目的与重要性
仿真分析的目的在于通过数学模型和算法预测和评估实际物理现象。对于机械结构而言,仿真分析可以帮助工程师预测结构性能和安全性,从而在产品开发阶段优化设计、降低风险和成本。
3.3 仿真分析案例研究
让我们通过一个典型的机械结构分析案例来进一步了解这一过程。
3.3.1 典型机械结构的分析案例
假设我们有一个机械臂设计,需要通过仿真来预测其在实际工作条件下的性能。我们将介绍如何使用有限元方法(FEM)来分析这个机械臂的结构响应。
首先,我们根据实际工作环境,设置机械臂所承受的各种载荷和边界条件。例如,机械臂在工作过程中可能会受到不同方向的力、力矩、温度变化等。通过模拟这些条件,我们可以在没有实际制造和测试物理模型的情况下,预测机械臂的性能。
接下来,我们选择合适的材料属性,包括弹性模量、泊松比、热膨胀系数等,并将这些参数输入到有限元分析软件中。
3.3.2 案例分析结果的解释与应用
完成分析后,我们得到一系列结果数据和图形。通过观察应力分布云图,我们可以判断哪些部分是结构的薄弱环节,可能需要加强。通过分析位移和变形图,我们可以了解机械臂在承受载荷时的移动和变形情况。如果发现某部分超过了材料的屈服极限,那么就需要重新设计该部分以避免潜在的破坏。
利用这些分析结果,我们还可以进行热力学分析,预测在高温或冷热循环工况下,机械臂材料的热应力和变形情况,以及疲劳分析来预测长期使用的可靠性。
为了提供一个更加丰富的章节内容,这里给出一个简单的几何模型构建示例,以及相关的代码块、表格和流程图。
假设我们要为一个简单的梁结构创建一个几何模型,并使用ANSYS进行分析。我们可以采取以下步骤:
设定模型的基本尺寸(例如长、宽、高)。 在ANSYS中输入这些尺寸,并使用块构建命令创建实体模型。 对模型进行网格划分,以便进行有限元分析。
在ANSYS中,这可以使用如下命令实现:
/prep7
et,1,SOLID185 ! 选择单元类型
block,0,100,0,50,0,20 ! 创建一个长100单位,宽50单位,高20单位的块体
esize,5 ! 设置网格尺寸为5单位
vmesh,1 ! 对块体进行网格划分
以上命令是ANSYS中的APDL(ANSYS Parametric Design Language)语言编写的,用于定义几何模型和网格划分。
下面是使用APDL创建的简单梁模型的参数表:
| 参数名称 | 描述 | 单位 | 数值 | |-----------|--------|-------|--------| | Length | 梁的长度 | 单位 | 100 | | Width | 梁的宽度 | 单位 | 50 | | Height | 梁的高度 | 单位 | 20 | | Element Type | 选用的单元类型 | - | SOLID185 | | Mesh Size | 网格尺寸 | 单位 | 5 |
在mermaid流程图中展示上述过程如下:
graph TD
A[开始构建几何模型] --> B[设定尺寸]
B --> C[创建块体结构]
C --> D[网格划分]
D --> E[模型准备就绪]
以上就是第三章关于机械结构仿真分析的详细内容,通过理论基础、仿真分析的目的重要性以及具体案例研究来逐步深入理解。接下来的内容将进一步探讨几何模型构建与管理、材料属性设定以及网格划分技巧等关键环节。
4. 几何模型构建与管理
在有限元分析(FEM)中,几何模型的构建和管理是关键的第一步,直接影响到整个仿真的精确度和效率。本章将深入探讨几何建模技术的概览、模型的优化与修正,以及管理策略,以确保读者能够掌握在ANSYS软件中有效操作几何模型的技巧。
4.1 几何建模技术概览 4.1.1 参数化与直接建模方法
在构建几何模型时,工程师可以选择参数化建模方法或直接建模方法。参数化建模通过定义一组参数来控制几何形状,这种方法可以轻松修改尺寸和形状,非常适合需要多次迭代和优化的设计过程。
flowchart LR
A[参数化建模] -->|定义参数| B[控制几何形状]
B --> C[易于修改与优化]
D[直接建模] -->|手动编辑| E[修改几何形状]
C -->|适应设计需求| F[快速迭代]
E -->|适应设计需求| F
直接建模方法则允许工程师直接在现有模型上进行修改,这种直观的方式在进行复杂模型修改时更为方便。但在参数化建模中,随着设计迭代的增加,参数之间的关系可能会变得复杂,需要精确控制以避免错误。
4.1.2 几何修复与模型简化
在现实世界中,获取的CAD模型往往包含很多不必要的细节和几何错误,这些都需要在进行有限元分析之前进行修复和简化。几何修复包括识别并修正面的重叠、间隙、非流形边等问题。模型简化通常涉及去除对分析结果影响较小的细节,以减少计算资源的消耗。
graph TD
A[获取CAD模型] --> B[识别几何错误]
B --> C[几何修复]
C --> D[模型简化]
D --> E[确保精度与效率平衡]
4.2 几何模型的优化与修正 4.2.1 模型精确度与计算效率的平衡
在有限元分析中,模型精确度和计算效率之间需要取得平衡。过于复杂的模型会消耗更多的计算资源,延长计算时间,而过于简化的模型则可能无法准确反映真实物理行为。工程师必须根据分析的目的,决定保留哪些细节,去除哪些不重要的特征。
4.2.2 模型错误检测与修正技巧
模型的错误检测和修正需要工程师具备一定的经验和直觉。常见的错误包括模型不封闭、单元质量差、网格扭曲等。这些错误可以通过ANSYS中的诊断工具识别,并利用其提供的修正工具进行修复。
graph LR
A[检测模型错误] --> B[识别问题]
B --> C[使用修正工具]
C --> D[修正模型]
D --> E[验证修正结果]
4.3 几何模型管理策略 4.3.1 多学科协同设计与模型共享
随着工程项目越来越复杂,多学科协同设计成为了必然趋势。几何模型需要支持从不同学科的工程师中进行共享和管理,以确保设计的一致性。ANSYS Workbench平台提供了一个集成环境,可以实现多学科数据的整合与共享。
4.3.2 模型版本控制与变更管理
为了确保设计的准确性和跟踪设计变更,有效的模型版本控制和变更管理至关重要。这可以通过版本控制系统来实现,如ANSYS提供与主流版本控制系统(如Git和SVN)的接口,帮助工程师维护不同版本的几何模型,并追踪模型的变更历史。
graph LR
A[开始设计] --> B[版本控制初始化]
B --> C[设计变更]
C --> D[提交新版本]
D --> E[比较版本差异]
E --> F[回归测试]
F -->|确认无误| G[更新主版本]
F -->|存在问题| H[回滚至旧版本]
综上所述,几何模型的构建与管理在有限元分析中占据着举足轻重的地位。合理地运用参数化建模、直接建模技术,以及通过版本控制和协同设计工具来管理几何模型,对于提升仿真的效率与准确性至关重要。在下一章节中,我们将进一步探讨材料属性设定在仿真分析中的作用,继续深入理解ANSYS软件在工程仿真领域的强大能力。
5. 材料属性设定 5.1 材料模型与特性 5.1.1 材料属性的分类与选择
在进行有限元分析时,选择合适的材料模型和属性是至关重要的。材料属性包括但不限于弹性模量、泊松比、密度、热导率等。为了模拟材料在不同加载条件下的行为,需要根据材料类型和预期的工程应用选择恰当的材料模型。
5.1.1.1 弹性材料模型
对于大多数工程应用来说,弹性模型是基础。弹性模型假设材料在弹性范围内加载卸载,不发生永久形变。常见的弹性模型包括:
5.1.1.2 塑性材料模型
当材料在受到超出其弹性极限的应力时,将进入塑性状态。塑性模型通常需要定义屈服准则,如冯·米塞斯屈服准则、特雷斯卡屈服准则等。
5.1.1.3 高级材料模型
在一些特殊的工程应用中,如高温环境、高速冲击等,可能需要使用如粘塑性模型、蠕变模型、复合材料模型等高级材料模型。
5.1.1.4 复合材料
对于由多种材料组成、具有各向异性特点的复合材料,需要采用复合材料模型进行分析。复合材料模型需要输入如纤维方向、层间剪切模量等特殊属性。
5.1.2 复杂材料模型的构建与应用
对于具有非线性行为或复杂结构的材料,构建准确的材料模型是仿真分析中的一个挑战。
5.1.2.1 材料非线性行为的建模
非线性行为包括但不限于塑性、粘弹性、疲劳等。在构建这些模型时,需要通过实验来确定材料的非线性特性,并将其转换成数学模型以供仿真软件使用。
5.1.2.2 材料模型的验证与优化
为了确保仿真结果的准确性,必须对材料模型进行验证。这通常涉及将仿真结果与实验数据进行对比,并调整模型参数直到达到满意的预测精度。
5.2 材料数据的获取与校准 5.2.1 实验数据的采集与处理
在材料模型中使用的关键参数需要通过实验获得。这些实验包括但不限于拉伸测试、压缩测试、疲劳测试等。
5.2.1.1 材料参数的实验测定
实验测定材料参数是一个精确和细致的过程,需要在严格控制的条件下进行。例如,在进行拉伸测试时,必须确保加载速度和测试温度符合预定标准。
5.2.2 材料模型的验证与优化 5.2.2.1 参数校准
参数校准是通过一系列迭代过程,将仿真结果与实验数据进行对比,调整模型参数以达到最佳拟合。这一过程可能需要借助优化算法来自动完成。
5.3 材料属性在仿真中的应用 5.3.1 不同工况下的材料属性应用
在仿真分析中,同一个材料在不同的工况下可能会表现出不同的属性。例如,温度变化可能会影响材料的弹性模量。
5.3.1.1 温度对材料属性的影响
对于温度敏感的材料,温度变化可能导致材料属性显著变化。在进行热力学分析时,这种温度依赖性需要被考虑在内。
5.3.2 材料非线性行为的模拟与分析 5.3.2.1 非线性材料模型的应用
在复杂的工程应用中,如汽车碰撞、结构大变形等,材料的非线性行为必须被精确模拟。非线性分析通常需要更多的计算资源和时间。
5.3.2.2 模拟分析与结果解释
模拟分析完成后,需要仔细检查和解释结果。重点关注材料的非线性行为,以及其对结构性能和安全性的影响。通过可视化工具,如等值线图、应力分布图等,帮助工程师理解材料在复杂工况下的响应。
6. 网格划分技巧
网格划分是有限元分析过程中至关重要的一步,它直接影响到分析的精度和计算效率。本章节将详细介绍网格类型的选择、细化与质量控制以及高级应用策略。
6.1 网格类型与选择标准 6.1.1 结构化与非结构化网格的优劣
结构化网格 通常用于几何形状简单的模型,例如规则的块体或板结构。它们的排列是有序的,便于处理,同时由于节点排列的规律性,有助于快速计算,提高求解精度。然而,对于复杂的模型,如具有复杂边界或内部空腔的模型,结构化网格可能难以适用。
非结构化网格 提供了更大的灵活性,可以适应各种复杂模型的表面或体积。它们可以是四边形、三角形、六面体或四面体等形状,适用于任何形状的几何模型。虽然非结构化网格的计算效率可能低于结构化网格,但它们提供了更好的模型适应性和通用性。
6.1.2 网格尺寸与分布对结果的影响
网格尺寸是影响计算精度和计算时间的关键因素。较细的网格可以提供更精确的结果,但也显著增加计算量。相对地,较大的网格会导致计算速度加快,但会牺牲一定的精度。
网格的分布也很重要,关键区域(如应力集中区域)需要更细的网格以捕捉详细信息,而非关键区域的网格可以较为稀疏。通过这样的调整可以平衡精度和计算效率。
flowchart LR
A[开始网格划分]
B[定义关键区域]
C[细网格划分]
D[非关键区域]
E[粗网格划分]
F[检查网格质量]
G[调整网格]
H[完成网格划分]
A --> B
B --> C
B --> D
C --> F
D --> E --> F
F --> G --> H
6.2 网格细化与质量控制 6.2.1 网格细化技术与智能划分
网格细化技术 包括自适应网格细化和基于特定标准的手动细化。自适应网格细化通常在迭代过程中进行,根据误差指标自动调整网格的密集程度。手动细化则需要工程师根据经验和模型特点进行决策。
智能划分技术,如ANSYS中的Meshing工具,可以自动选择最优的网格类型和大小,同时提供网格质量的实时反馈。
6.2.2 网格质量评估与改进策略
网格质量评估是一个必须的步骤,主要通过以下几个方面:
根据评估结果,可以采取以下改进策略:
6.3 网格划分的高级应用 6.3.1 多尺度网格划分技术
多尺度网格划分技术允许在模型的不同区域应用不同尺度的网格。这对于包含宏观和微观结构的复杂模型特别有用。例如,在宏观模型中使用较大网格来提高计算效率,在需要详细分析的微观区域使用较小网格以捕捉关键信息。
6.3.2 自适应网格技术在复杂模型中的应用
自适应网格技术通过分析误差指标并迭代调整网格来优化分析结果。在有限元分析中,自适应网格可以显著提高关键区域的分析精度,同时保持整个模型的计算效率。
自适应网格技术需要足够的计算资源,因为它们通常需要多次计算迭代,但是通过智能算法,如ANSYS提供的工具,可以实现更精确和有效的分析。
在下一章节,我们将继续深入了解边界条件与载荷定义,以及它们在仿真分析中的应用和重要性。

简介:本文档为初学者提供了一份关于ANSYS有限元分析的全面介绍,涵盖了有限元方法(FEM)的基础知识、软件操作流程及机械结构仿真分析。内容包括有限元方法在工程问题中的应用、ANSYS软件的使用、模型构建、材料属性设置、网格划分、边界条件与载荷定义以及结果分析和解释。旨在帮助学习者通过系统学习提升解决实际工程问题的能力。